Finite Sets and Infinite Sets – Foundations of Mathematics

Grab some collection of objects and count it. How does that work?

Let's say we want to count the (living) former Presidents of the United States in this photograph:

We're so good at counting that we'd probably just glance and say "5". But if we were three or four years old, we'd probably have to count more carefully, which means doing something like placing our index finger on Obama and pronouncing "one", shifting the index finger to W. Bush and pronouncing "two", shifting the index finger to Clinton and pronouncing "three", shifting it to H. W. Bush and pronouncing "four", and finally shifting to Carter and pronouncing "five".

In other words, we would construct the following explicit bijection:

$Obama\ \ \mapsto 1\\W Bush\ \ \mapsto 2\\ Clinton\ \ \mapsto 3\\ HW Bush\ \ \mapsto 4\\Carter\ \ \mapsto 5$

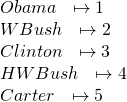
Definition. We call the set A finite if either A is empty, or there is some $k\in\mathbb{N}$ and a bijection $f:A\rightarrow \{1,2,\ldots, k\}$ . The number $k$ is called the cardinality of A. The cardinality of the empty set is defined to be 0.

We've been dealing with finite sets our whole lives, and much of set theory is inspired by them. We'll take the time to record some important facts, which may seem obvious but are worth noting.

Theorem. If $A$ is finite and there is a surjection $g:A\rightarrow B$ , then $B$ is finite.

Proof. We'll start with a lemma:

Lemma. If there is a surjection $g:A\rightarrow B$ , then there is an injection $h:B\rightarrow A$ .

Proof. Since $g$ is a surjection, for each $b\in B$ , there is some $a\in A$ with $g(b)=a$ . Pick one of them and call it $h(b)$ .

We claim $h:B\rightarrow A$ is an injection. $\Box$ .

So now we have an injection $h$ from $B$ to a finite set. Further, there is some bijection $\psi:A\rightarrow\{1,\ldots,n\}$ . Then $\psi\circ h:B\rightarrow \{1,\ldots, n\}$ is an injection. But every function is a surjection onto its range, so $B$ is bijective with a subset of $\{1,\ldots,n\}$ , hence must be finite. $\Box$

Corollary. If $A$ is finite and there is an injection $h:B\rightarrow A$ , then $B$ is finite.

Corollary. Any subset of a finite set is finite.

Proof. If $X\subseteq Y$ and $Y$ is finite, consider the function $\iota_X:X\rightarrow Y$ given by $\iota_X:t\mapsto t$ . This is an injection, so the previous corollary applies. $\Box$ .

Definition. We call $B$ a proper subset of $A$ if $B\subseteq A$ but $B\neq A$ ; that is, if every element of $B$ is an element of $A$ , but there is some element of $A$ which is not an element of $B$ .

Theorem. If $A$ is finite, then $A$ is not equivalent to any of its proper subsets.

Proof. Suppose not. Then there is some finite set $A$ and a proper subset $B$ of $A$ with $B\approx A$ . So there is some $a_0\in A$ with $a_0\notin B$ .

Now let $\psi: A\rightarrow \{1,\ldots, n\}$ be the bijection which shows that $A$ is finite, and arrange so that $\psi(a_0)=n$ . Then the range of $\psi|_B$ is a subset of $\{1,\ldots, n-1\}$ . But then $\{1,\ldots, n\}$ would be equivalent to a subset of $\{1,\ldots, n-1\}$ , which is absurd. $\Box$ .

Perhaps the most surprising part of this theorem is that we have the assumption `` $A$ is finite". You might think that there's no way a set could be equivalent to the set you get after you remove an element. But! Infinite sets are kind of weird; or at least we aren't used to dealing with them so our intuitions are sometimes wrong.

Definition. We call a set $A$ infinite if it is not finite.

Theorem. If $A$ is equivalent to one of its proper subsets, then $A$ is infinite.

Proof. This is the contrapositive of the last theorem.

This theorem (though you might think its hypothesis never applies) turns out to be a very useful way to prove that a particular set is infinite.

Theorem. $\mathbb{N}$ is infinite.

Proof. Consider the function $f:n\mapsto n+1$ . This is a function from $\mathbb{N}$ to $\mathbb{N}\setminus\{1\}$ . Notice that there is a function $g:\mathbb{N}\setminus\{1\}\rightarrow \mathbb{N}$ given by $g(p)=p-1$ , which has

$\begin{align*}g(f(n))&=g(n+1)=n+1-1=n\\f(g(p))&=f(p-1)=p-1+1=p\end{align*}$

so that $g$ serves as an inverse to $f$ . Therefore $f$ is a bijection, and so $\mathbb{N}\approx\mathbb{N}\setminus\{1\}$ . $\Box$

We can also give another proof, which is how most proofs that something is infinite go. Since infinite just means not finite, we challenge the reader to try and tell us how many elements the infinite set has. Then we show we can always defeat them, by finding an element they left out of their count.

Another proof that $\mathbb{N}$ is infinite.

Suppose $\mathbb{N}$ had finitely many elements, say $K$ of them. Then there would be a bijection $\psi:\{1,\ldots,K\}\rightarrow \mathbb{N}$ .

Let $L=\psi(1)+\psi(2)+\cdots+\psi(K)$ . Then $L$ is strictly greater than any of the $\psi(i)$ . Therefore $L\notin \operatorname{Range}(\psi)$ . so $\psi$ is not onto. This contradiction establishes the theorem. $\Box$ .

The following proof of this type is the oldest recorded reductio ad absurdum.

Theorem. (Euclid, ca. 300 BCE) There are infinitely many prime numbers.

Proof. Suppose there were finitely many prime numbers, say $K$ of them. List them all: $p_1,\ldots, p_K$ . Consider the numbers

$\begin{align*}L&=p_1p_2\cdots p_K\\M&=L+1 \end{align*}$

Now we know that $M$ has at least one prime factor; call that factor $q$ . Observe that $q$ could not be 2, because $L$ is even, so $M$ is odd. Further, $q$ could not be 3, because $L$ is a multiple of 3, so $M$ has remainder 1 when we divide by 3. Proceeding in this way, we find that $q$ cannot be any of the prime numbers we listed.

So we have found a prime that was not on our list, which we supposed to be complete. This contradiction establishes the theorem. $\Box$ .

We can also show that a set is infinite by finding an infinite subset:

Theorem. If $A\subseteq B$ and $A$ is infinite, then $B$ is infinite.

Proof. Assume $A\subseteq B$ . We will show that if $A$ is infinite, then $B$ is infinite. The contrapositive of this claim is: If $B$ is finite, then $A$ is finite, which we already showed. $\Box$

E.g. $\mathbb{R}$ is infinite.

Actually this can be souped up:

Theorem. If $A$ is infinite and there is an injection $\psi:A\rightarrow B$ , then $B$ is infinite.

E.g. $\mathbb{N}\times\mathbb{N}$ is infinite.

Proof. Consider the function $\psi:\mathbb{N}\rightarrow \mathbb{N}\times\mathbb{N}$ given by $\psi(k)=(k,k)$ .

If $\psi(k_1)=\psi(k_2)$ , then $(k_1,k_1)=(k_2,k_2)$ , so $k_1=k_2$ . This shows that $\psi$ is an injection, so the above theorem shows that $\mathbb{N}\times \mathbb{N}$ is infinite. $\Box$

$\mathbb{N}$ is in fact the smallest infinite set, in the following sense:

Theorem. Any infinite set has a subset which is equivalent to $\mathbb{N}$ .

Proof. Let $X$ be an infinite set. We'll show, by induction, that we can pick a distinct element $x_n\in X$ for each $n\in\mathbb{N}$ .

For the base case, pick $x_1\in X$ . Note that $X\setminus\{x_1\}$ is not empty (otherwise $X$ would have had only one element to begin with).

For the inductive step, suppose we've picked $x_1,\ldots,x_k$ distinct elements of $X$ already. Then $X\setminus\{x_1,\ldots, x_k\}$ is not empty (otherwise $X$ would have only $k$ elements), so there is some $x_{k+1}\in X$ which is distinct from $x_1,\ldots,x_k$ .

Mathematical induction allows us to continue this way to define $x_n$ for any $n\in\mathbb{N}$ , thus building a bijection $\mathbb{N}\rightarrow \{x_1,\ldots,x_n,\ldots\}$ . $\Box$ .