Recall that we defined inverses for any relation:
Definition. If ![]() is a relation from
is a relation from ![]() to
to ![]() , then
, then ![]() is a relation from
is a relation from ![]() to
to ![]() , defined by
, defined by ![]() iff
iff ![]() .
.
Thus (in our formalism) every function has an inverse. The inverse of a function so defined, however, may not be a function itself! (Remember that most operations we do to sets or to relations will not preserve functionhood.) So let's discover when taking the inverse (``swapping ![]() and
and ![]() ") actually does result in a function.
") actually does result in a function.
Recall that ![]() means that two conditions hold:
means that two conditions hold:
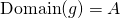
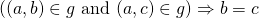 .
.
Exercise 1. Suppose ![]() . By substituting
. By substituting ![]() for
for ![]() ,
, ![]() for
for ![]() , and
, and ![]() for
for ![]() , write what it means for
, write what it means for ![]() .
.
Exercise 2. Use the definition of ![]() to rewrite your conditions solely in terms of
to rewrite your conditions solely in terms of ![]() (with no
(with no ![]() anywhere).
anywhere).
Definition. Let ![]() . We call
. We call ![]() onto or surjective if
onto or surjective if ![]() . We call
. We call ![]() one-to-one or injective if for any
one-to-one or injective if for any ![]() , we have that
, we have that ![]() guarantees
guarantees ![]() .
.
Definition. A function which is both one-to-one and onto is called a one-to-one correspondence or a bijection.
The following theorem is important, but its proof is just the combination of Exercises 1 and 2.
Theorem. Let ![]() . Then
. Then ![]() iff
iff ![]() is both one-to-one and onto.
is both one-to-one and onto.
Theorem. Suppose ![]() is one-to-one and
is one-to-one and ![]() is one-to-one. Then
is one-to-one. Then ![]() is one-to-one.
is one-to-one.
Proof. Note that the condition that ![]() be defined on the range of
be defined on the range of ![]() is necessary in order to compose the two functions as functions.
is necessary in order to compose the two functions as functions.
Let ![]() . Suppose
. Suppose ![]() . Applying the fact that the composition of functions is a function, we have
. Applying the fact that the composition of functions is a function, we have
![]()
Since ![]() is one-to-one, we have
is one-to-one, we have ![]() . Since
. Since ![]() is one-to-one, we have
is one-to-one, we have ![]() . Since
. Since ![]() were arbitrary, we've shown
were arbitrary, we've shown ![]() is one-to-one.
is one-to-one. ![]() .
.
Theorem. Suppose ![]() is onto and
is onto and ![]() is onto. Then
is onto. Then ![]() is onto.
is onto.
Proof. This is an exercise for you.
