Denumerable Sets – Foundations of Mathematics

We know that $\mathbb{N}$ is the smallest infinite set; this makes $\mathbb{N}$ a pretty good place to get started. But our ideas about size have to do just with bijections, so whatever we'd say about $\mathbb{N}$ we could also say about any set which is equivalent to $\mathbb{N}$ .

Definition. If $X\approx \mathbb{N}$ , we call $X$ denumerable, and we call any bijection $\psi:X\rightarrow \mathbb{N}$ a denumeration of $X$ . We call $X$ countable if it is either finite or denumerable. Sometimes denumerable sets are called countably infinite.

E.g. $\mathbb{N}$ is denumerable.

Theorem. Any subset of a denumerable set is countable.

Proof. Let $X$ be denumerable and $A\subseteq X$ . Assume that $A$ is not finite; we'll show that $A$ is denumerable.

Since $X$ is denumerable, there is a bijection $\psi:X\rightarrow\mathbb{N}$ . We'll construct a denumeration of $A$ using induction.

For the base case: by the Well-Ordering Principle, there is a least element of $\psi_*(A)$ . By injectivity, this element is the image of a unique element of $A$ , call it $a_1$ . Observe that $A\setminus\{a_1\}$ is not empty, so $\psi_*(A\setminus\{a_1\})$ is not empty.

Suppose we've denumerated $k$ elements of $A$ so far, say $a_1,\ldots, a_k$ . Since $A$ is not finite, $A\setminus\{a_1,\ldots a_k\}$ is not empty. So $\psi_*(A\setminus\{a_1,\ldots,a_k\})$ is a nonempty subset of $\mathbb{N}$ , hence by the Well-Ordering Principle has a least element. By injectivity, this element is the image of a unique $a_{k+1}\in A$ , which is distinct from all the $a_1,\ldots, a_k$ .

Proceeding in this way, we construct a bijection $\mathbb{N}\rightarrow \{a_1,\ldots, a_n,\ldots\}$ . Moreover, any $a\in A$ will be one of the $a_k$ , since $\psi(a)$ will occur in the list of values. So we have $\mathbb{N}\approx A$ . $\Box$ .

Corollary. The following sets are equivalent to $\mathbb{N}$ :

The set of prime numbers.
The set of even natural numbers.
The set of odd natural numbers.
The set of positive powers of 2.
The set of positive powers of 3.

Proof. These are all infinite subsets of $\mathbb{N}$ . Since they're not finite, they must be denumerable. $\Box$ .

Theorem. Any subset of a countable set is countable.

Theorem. If $B$ is countable and there is an injection $g:A\rightarrow B$ , then $A$ is countable.

Theorem. If $A$ is countable and there is a surjection $g:A\rightarrow B$ , then $B$ is countable.

One weird thing about denumerable sets -- actually any infinite set -- is that if you add a single element, the set doesn't get any larger.

Theorem. $\mathbb{N}\approx\mathbb{N}\cup\{0\}$ .

Proof. The bijection is given by sending $n\in\mathbb{N}$ to $n-1\in\mathbb{N}\cup\{0\}$ . $\Box$ .

Okay, but what if we tried to add an entire additional copy of $\mathbb{N}$ -- say, the negative numbers.

Theorem. $\mathbb{Z}\approx \mathbb{N}$ .

Proof. We'll give a bijection $\mathbb{N}\cup\{0\}\rightarrow \mathbb{Z}$ . Try

$\begin{align*}\mathbb{N}\cup\{0\}&\rightarrow \mathbb{Z}\\n&\mapsto\begin{cases}-\frac{n}{2} & \text{ if }n \text{ is even}\\\frac{n+1}{2} & \text{ if }n\text{ is odd}\end{cases}\end{align*}$

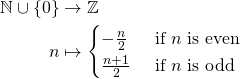
As an exercise, show that this function is a bijection. Actually, givetwo proofs: one by showing it is injective and surjective, and one by building the inverse function. $\Box$ .

Notice that this is a bit weird: $\mathbb{Z}=\mathbb{N}\cup(\mathbb{N}\cup\{0\})$ is the union of two disjoint sets, each of which is equivalent to $\mathbb{N}$ . But it's no bigger than $\mathbb{N}$ .

Theorem. If $A$ is denumerable and $B$ is denumerable, then $A\times B$ is denumerable.

Proof. We'll show first that $\mathbb{N}\times\mathbb{N}$ is denumerable.

We can represent $\mathbb{N}\times\mathbb{N}$ as a grid of points in the plane:

Rendered by QuickLaTeX.com

and then denumerate them in any order we like, starting perhaps from the origin and snaking around like so:

Rendered by QuickLaTeX.com

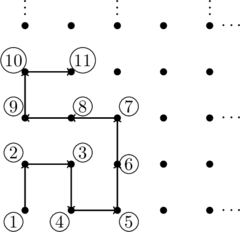
It's clear that we'll eventually get all the dots numbered (so our denumeration is onto), and that dot will only get one number (so our denumeration is one-to-one).

Now let's go from this special case to the general case.

Lemma. If $A\approx B$ and $X\approx Y$ , then $A\times X\approx B\times Y$ .

Proof. This is homework. $\Box$ .

To complete the proof: we know that $A$ and $B$ are denumerable, so we have $A\approx \mathbb{N}$ and $B\approx \mathbb{N}$ . So by the lemma $A\times B\approx \mathbb{N}\times\mathbb{N}$ . But we showed $\mathbb{N}\times\mathbb{N}\approx\mathbb{N}$ . So by transitivity of $\approx$ , we have $A\times B\approx\mathbb{N}$ . $\Box$ .

Theorem. If $A$ is countable and $B$ is countable, then $A\times B$ is countable.

Proof. We have the cases when both sets are finite and both sets are denumerable. So we only need to handle the case when one set is finite and the other is denumerable. This is an exercise. $\Box$ .

Theorem. $\mathbb{Q}$ is denumerable.

Proof. By the theorem above, $\mathbb{Z}\times\left(\mathbb{Z}\setminus\{0\}\right)$ is countable. There is a surjection from $\mathbb{Z}\times\left(\mathbb{Z}\setminus\{0\}\right)$ to $\mathbb{Q}$ given by $(m,n)\mapsto \frac{m}{n}$ , so $\mathbb{Q}$ is countable. But we have an injection from $\mathbb{N}$ to $\mathbb{Q}$ given by $n\mapsto\frac{1}{n}$ , so $\mathbb{Q}$ is infinite. $\Box$ .