Definition. A function ![]() from a set
from a set ![]() to a set
to a set ![]() is a relation which satisfies the following two conditions:
is a relation which satisfies the following two conditions:
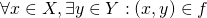 , and
, and![Rendered by QuickLaTeX.com \forall x\in X, y_1,y_2\in Y, \left[(x,y_1)\in f \wedge (x,y_2)\right]\in f\Rightarrow y_1=y_2](https://ma225.wordpress.ncsu.edu/wp-content/ql-cache/quicklatex.com-222795e71676dda2297d754f58f97cdf_l3.png)
That is, a function assigns to each (clause 1) element of ![]() an element of
an element of ![]() , and that assignment is unambiguous (clause 2). Since we could rewrite clause 1 as
, and that assignment is unambiguous (clause 2). Since we could rewrite clause 1 as ![]() (why?), we'll refer to clause 1 as the "domain clause" and clause 2 as the "unambiguousness clause".
(why?), we'll refer to clause 1 as the "domain clause" and clause 2 as the "unambiguousness clause".
Notation. Instead of the mouthful ![]() is a function from
is a function from ![]() to
to ![]() , we write the shorthand
, we write the shorthand ![]() .
.
We also have this familiar notation:
Notation. If ![]() is a function from
is a function from ![]() to
to ![]() , and
, and ![]() , we write
, we write ![]() .
.
Observe that if ![]() and
and ![]() , then this notation reads as follows:
, then this notation reads as follows: ![]() and
and ![]() , so we'd darn well better have
, so we'd darn well better have ![]() , or else something is very wrong.
, or else something is very wrong.
There is another way to represent a function, by specifying its domain and its rule:
Notation. If ![]() is a function from
is a function from ![]() to
to ![]() , we write
, we write ![]() . To specify the rule that
. To specify the rule that ![]() uses, we write
uses, we write
![]()
For example, we could denote the function which takes in a real number as input, and squares it by
![]()
Notice that the arrow between the sets is a different shape from the one between elements of the set. As usual we want to let go of our ![]() s, so we could as well have written
s, so we could as well have written
![]()
or
![]()
This frees us from the tyranny of always writing ![]() .
.
