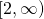When are two functions equal? A function is a kind of relation, which means it's a kind of set. So two functions being equal means, fundamentally, that each is a subset of the other. That's inconvenient, and it doesn't really jibe with our understanding of functions as encoding rules.
Theorem About When Functions Are Equal (TAWFAE). Let ![]() and
and ![]() be functions. Then
be functions. Then ![]() if and only if:
if and only if:
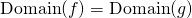 , and
, and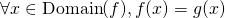 .
.
Proof. This theorem sort of looks like it will be complicated to prove, but let's keep our wits about us and rely on logic to help us out.
Globally, this is a biconditional proof so it has two directions:
(![]() ) Assume
) Assume ![]() . We need to prove two things:
. We need to prove two things:
(clause 1) This is the claim that two sets are equal, so we have to prove each is a subset of the other:
(![]() ) Let
) Let ![]() . Then
. Then ![]() . Since
. Since ![]() , this means
, this means ![]() . So
. So ![]() .
.
(![]() ) Let
) Let ![]() . Then
. Then ![]() . Since
. Since ![]() , this means
, this means ![]() . So
. So ![]() .
.
(clause 2) This is a universal claim, so we start the same way as always: Let ![]() . Then
. Then ![]() . We can rewrite this as
. We can rewrite this as ![]() . On the other hand, we know from clause 1 that
. On the other hand, we know from clause 1 that ![]() , so
, so ![]() . We can rewrite this as
. We can rewrite this as ![]() . But since
. But since ![]() , we actually have
, we actually have ![]() .
.
Since ![]() and
and ![]() , and
, and ![]() is a function,
is a function, ![]() .
.
So ![]() .
.
(![]() ) Assume both clauses 1 and 2 hold. In this direction, we need to prove two sets are equal.
) Assume both clauses 1 and 2 hold. In this direction, we need to prove two sets are equal.
(![]() ) Let
) Let ![]() . Then
. Then ![]() for some
for some ![]() and some
and some ![]() .
. ![]() , so by clause 1,
, so by clause 1, ![]() . Then there's some
. Then there's some ![]() with
with ![]() . We can rewrite in function notation as
. We can rewrite in function notation as ![]() and
and ![]() . By clause 2, we know
. By clause 2, we know ![]() , so
, so ![]() . That is,
. That is, ![]() .
.
(![]() ) This is so similar to
) This is so similar to ![]() , I'll let you work it out.
, I'll let you work it out.
Since we proved both directions, we're done. ![]() .
.
This theorem gives us a new way to prove two functions are equal, should we ever need it: we establish clause 1 ("they have the same domain") and clause 2 ("they have the same rule").
Restrictions and Extensions
In middle and high school algebra courses, we often ask questions like "What's the domain of ![]() ?". According to the TAWFAE, this is actually a dumb question: TAWFAE says in order to know what a function is, we need to know what the domain is. So a question like doesn't actually contain enough information to be answerable.
?". According to the TAWFAE, this is actually a dumb question: TAWFAE says in order to know what a function is, we need to know what the domain is. So a question like doesn't actually contain enough information to be answerable.
What the question is really asking, though is: what's the most natural, or maybe what's the largest possible domain on which this rule makes sense?
As a middle-school student, I was very confused by questions like this one:
Find the domain of ![]() .
.
My answer would usually go like this: that function is really the same as ![]() , the domain of which is all of
, the domain of which is all of ![]() . And I would always get that question wrong. Why?
. And I would always get that question wrong. Why?
The functions ![]() and
and ![]() do indeed have the same rule, in the sense that, whenever
do indeed have the same rule, in the sense that, whenever ![]() makes sense, we have
makes sense, we have
![]()
But the natural domain of ![]() is
is ![]() and the natural domain for
and the natural domain for ![]() is
is ![]() ; so that means the domains are different -- hence by the TAWFAE, we know
; so that means the domains are different -- hence by the TAWFAE, we know ![]() . Nevertheless, the two functions are related.
. Nevertheless, the two functions are related.
Definition. If ![]() and
and ![]() , we define the restriction of
, we define the restriction of ![]() to
to ![]() as
as
![]()
That is, ![]() has the same rule as
has the same rule as ![]() , just we only care about inputs that come from
, just we only care about inputs that come from ![]() .
.
Equipped with this notion, we can describe the relationship between ![]() and
and ![]() :
:
![]()
Definition. If ![]() , and
, and ![]() , and there is
, and there is ![]() with
with ![]() , we call
, we call ![]() an extension of
an extension of ![]() .
.
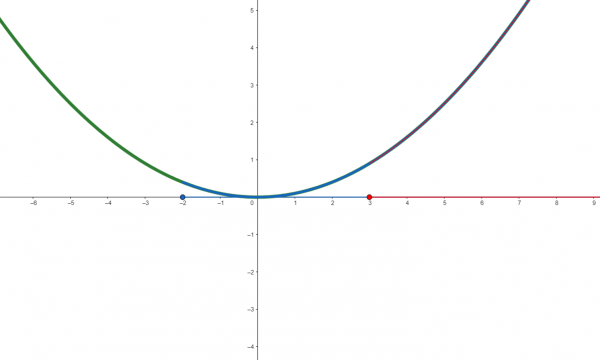
Here's an illustration: if we let ![]() denote the function displayed in green,
denote the function displayed in green, ![]() denote the function displayed in blue, and
denote the function displayed in blue, and ![]() the function displayed in red, then we have that:
the function displayed in red, then we have that:
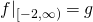
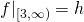
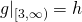
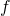 is an extension of
is an extension of 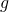 , from
, from 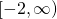 to all of
to all of 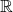
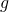 is an extension of
is an extension of 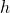 , from
, from 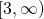 to
to