Set Operations on Functions
Functions are sets, so we can try to combine them like we combine sets. That is, we can ask the following questions:
- Is the complement of a function necessarily a function?
- Is the intersection of two functions necessarily a function?
- Is the union of two functions necessarily a function?
- Is the set product of two functions necessarily a function?
Let's investigate the first three; the last one I'll leave for homework.
To start with, let's pick two functions and run with them. How about: ![]() and
and ![]() .
.
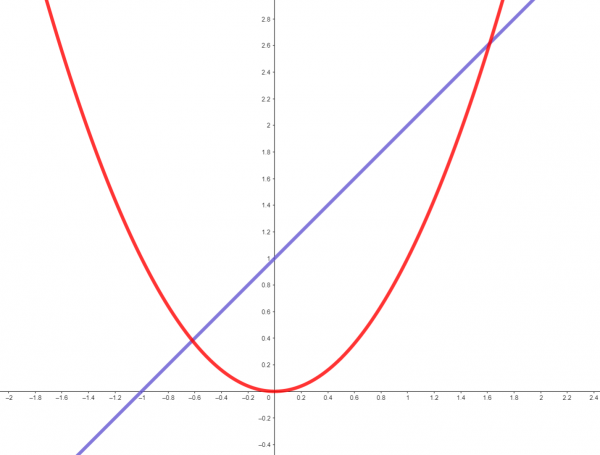
The complement of ![]() is
is ![]() , shown here in hatching:
, shown here in hatching: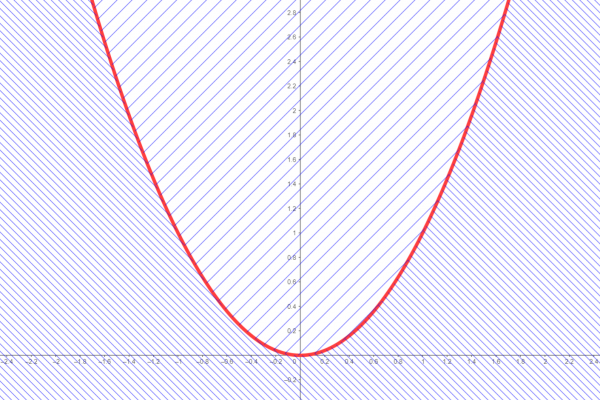 That's definitely not a function: it badly fails the vertical line test.
That's definitely not a function: it badly fails the vertical line test.
What about intersection?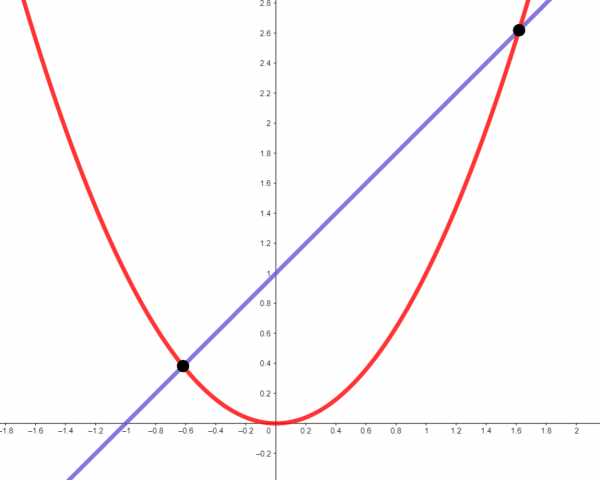
The intersection is just two points; so ![]() is not a function from
is not a function from ![]() to
to ![]() . But
. But ![]() is a function from a smaller set.
is a function from a smaller set.
Let's look at ![]() :
:
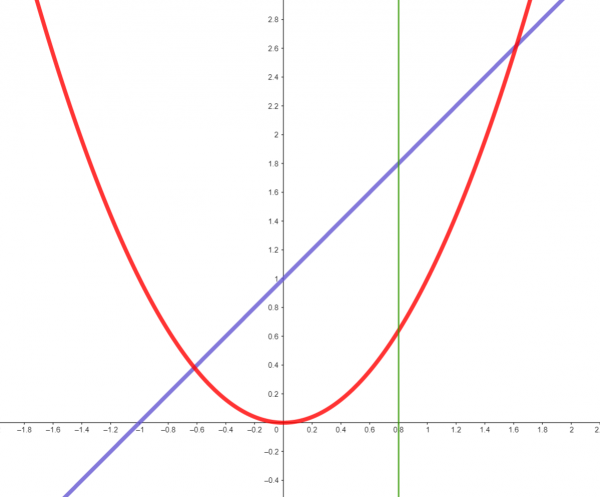
It also fails the vertical line test. But:
The Pasting Lemma (in the category of sets). Let ![]() and
and ![]() be two functions. Then
be two functions. Then ![]() if and only if
if and only if ![]() .
.
Proof. This is a biconditional, so we have two directions:
(![]() ) Assume
) Assume ![]() . We need to show
. We need to show ![]() is a function; to do this, there are two clauses.
is a function; to do this, there are two clauses.
(clause 1: domain) Let ![]() . Then either
. Then either ![]() or
or ![]() .
.
If ![]() , then because
, then because ![]() ,
, ![]() . Then
. Then ![]() .
.
If ![]() , then because
, then because ![]() ,
, ![]() . Then
. Then ![]() .
.
In either case, there's an element of ![]() so that
so that ![]() . That's clause 1 of the definition of function.
. That's clause 1 of the definition of function.
(clause 2: unambiguousness) Let ![]() and
and ![]() be such that
be such that ![]() and
and ![]() . There are four cases:
. There are four cases:
If ![]() and
and ![]() , then the fact that
, then the fact that ![]() is a function implies
is a function implies ![]() .
.
If ![]() and
and ![]() , then the fact that
, then the fact that ![]() is a function implies
is a function implies ![]() .
.
If ![]() and
and ![]() , then we have
, then we have ![]() and
and ![]() , so
, so ![]() . But then
. But then ![]() . So
. So ![]() . So
. So ![]() . Since
. Since ![]() is a function,
is a function, ![]() .
.
If ![]() and
and ![]() , then we have
, then we have ![]() and
and ![]() , so
, so ![]() . But then
. But then ![]() . So
. So ![]() . So
. So ![]() . Since
. Since ![]() is a function,
is a function, ![]() .
.
In any of these four cases, ![]() , which is what we needed for clause 2 of the definition of function.
, which is what we needed for clause 2 of the definition of function.
(![]() ) In this direction, we need to show two functions are equal. So we should probably use the TAWFAE. I'll leave this direction to you.
) In this direction, we need to show two functions are equal. So we should probably use the TAWFAE. I'll leave this direction to you.
Why does this theorem bear such a silly name? Consider this diagram, which tells you how to build a cube from a piece of paper. In order to attach the sides, you have to paste the red tab to the back of one of the appropriate square (I've indicated where the red tab gets attached by coloring it green). We won't succeed in pasting unless the red tab and the green target match up. 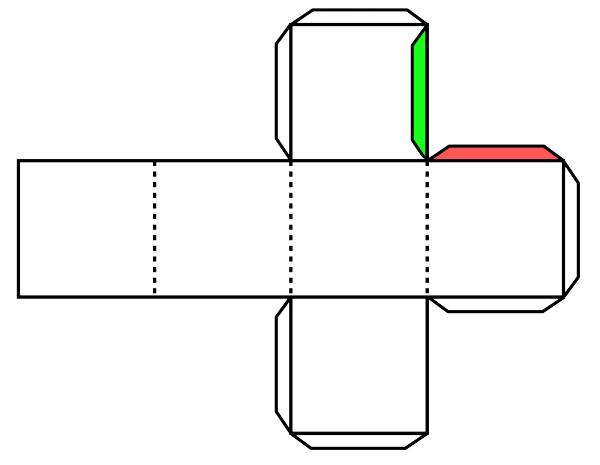
That's what the condition ![]() ensures: that the functions
ensures: that the functions ![]() and
and ![]() agree on the overlap of their domains.
agree on the overlap of their domains.
Again, an example from precalculus mathematics: when we define a function piecewise, like
![Rendered by QuickLaTeX.com \[h(x)=\begin{cases}x^2 & \text{ if } x\leq 3\\ -x+1&\text{ if } x>3\end{cases}\]](https://ma225.wordpress.ncsu.edu/wp-content/ql-cache/quicklatex.com-1c2e81bd5163209d38243890482fd9d5_l3.png)
we usually want to make sure that the two pieces have nonoverlapping domains. This corresponds, in the Theorem above, to the case that ![]() . If we weren't so careful, we might have a situation like this:
. If we weren't so careful, we might have a situation like this:
![Rendered by QuickLaTeX.com \[h(x)=\begin{cases}x^2 & \text{ if } x\leq 3\\ -x+1&\text{ if } x>1\end{cases}\]](https://ma225.wordpress.ncsu.edu/wp-content/ql-cache/quicklatex.com-337d5a18dbab3136329a91fe177c8d8c_l3.png)
where it's ambiguous what ![]() is:
is: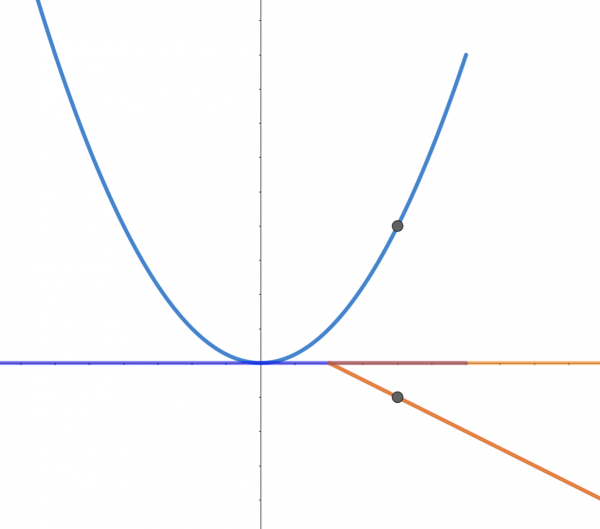
Composition of Functions
Because functions are relations, we can consider their composites. We have the following nice theorem:
The Composition of Functions Is a Function. If ![]() and
and ![]() , then
, then ![]() .
.
Proof. There are two things to show:
(clause 1: domain) Let ![]() . Then, because
. Then, because ![]() is a function,
is a function, ![]() . Since
. Since ![]() and
and ![]() is a function,
is a function, ![]() . Then
. Then ![]() .
. ![]() .
.
(clause 2: unambiguousness) Given ![]() so that
so that ![]() and
and ![]() . We need to show
. We need to show ![]() .
.
Since ![]() , there is some
, there is some ![]() with
with ![]() and
and ![]() . We also have
. We also have ![]() with
with ![]() and
and ![]() .
.
Since ![]() is a function,
is a function, ![]() . So we have
. So we have ![]() . But since
. But since ![]() is a function,
is a function, ![]() and
and ![]() forces
forces ![]() .
. ![]() .
.
Important Formula. If ![]() and
and ![]() are functions, so that
are functions, so that ![]() is a function, then
is a function, then ![]() .
.
Proof. What does it mean for ![]() ? It means
? It means ![]() . But that means
. But that means ![]() and
and ![]() . So
. So ![]() and
and ![]() . By substituting, we obtain
. By substituting, we obtain ![]() .
. ![]()
This formula explains the "backwards" looking choice of how we write compositions: even though ![]() come first, we write
come first, we write ![]() . The only way out of this would be to switch our function notation to something like
. The only way out of this would be to switch our function notation to something like ![]() , so that the composite would be
, so that the composite would be ![]() . (Some people do this, and it has a name: reverse Polish notation. But most normal people don't do it.)
. (Some people do this, and it has a name: reverse Polish notation. But most normal people don't do it.)
