All men are created equal.
Thomas Jefferson, Declaration of Independence
I don't hold with equality in all things, just equality before the law, nothing more.
character of Rep. Thaddeus Stevens in the film Lincoln
We ordinarily are completely comfortable writing things like
![]()
The symbols ![]() and
and ![]() , though, are definitely not the same. One of them, for example, has four digits in the denominator, whereas the other has only one digit in the denominator. So in what sense is it the case that these three symbols are the same? Intuitively, they represent the same thing.
, though, are definitely not the same. One of them, for example, has four digits in the denominator, whereas the other has only one digit in the denominator. So in what sense is it the case that these three symbols are the same? Intuitively, they represent the same thing.
Children are usually introduced to fractions as being parts of a whole. What is half a pizza? It's what happens when you divide one pizza into two parts. Then we think of fractions like ![]() as either: one piece, if you divide two pizzas into four parts, or two pieces if you divide one pizza into four parts. But these are manifestly not the same thing! Two halves of a Ming vase are not the same as a whole Ming vase, and if you ordered a pizza at the pizza shop, you'd be very upset when they brought out a pizza in a million little pieces.
as either: one piece, if you divide two pizzas into four parts, or two pieces if you divide one pizza into four parts. But these are manifestly not the same thing! Two halves of a Ming vase are not the same as a whole Ming vase, and if you ordered a pizza at the pizza shop, you'd be very upset when they brought out a pizza in a million little pieces.
Yet we write ![]() and don't really think about it. We're choosing to ignore some differences between two things, and treat them like they're equal. Like Thaddeus Stevens, we are not asserting equality in all things, only equality before the law (of fractions).
and don't really think about it. We're choosing to ignore some differences between two things, and treat them like they're equal. Like Thaddeus Stevens, we are not asserting equality in all things, only equality before the law (of fractions).
An equivalence relation is a way of formalizing this process of picking what to ignore and what to pay attention to.
Equality
The following properties are true for the identity relation ![]() (we usually write
(we usually write ![]() as
as ![]() ):
):
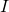 is {\em reflexive}: for any object
is {\em reflexive}: for any object 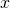 ,
,  (or
(or 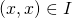 ).
).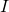 is {\em symmetric}: for any objects
is {\em symmetric}: for any objects 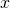 and
and 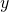 , if
, if 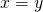 then it must be the case that
then it must be the case that 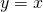 .
.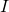 is {\em transitive}: for any objects
is {\em transitive}: for any objects 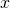 ,
, 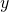 , and
, and  , if
, if 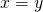 and
and 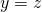 then it must be the case that
then it must be the case that 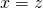 .
.
Equality also has the replacement property: if ![]() , then any occurrence of
, then any occurrence of ![]() can be replaced by
can be replaced by ![]() without changing the meaning. So for example, when we write
without changing the meaning. So for example, when we write ![]() , we know that
, we know that ![]() is false, because
is false, because ![]() is false.
is false.
Notice that Thomas Jefferson's claim that all men are created equal does not have this property. Michael Jackson is a man, and Bill Nye is a man, so if all men are equal, we should be able to replace any occurrence of ``Michael Jackson" with ``Bill Nye" without loss of meaning. It's true that
Michael Jackson is the King of Pop.
But we can't say that this means
Bill Nye is the King of Pop.
So it seems like we at least have to give up the replacement property, if we want to make sense of notions like equal before the law.
Equivalence
We want to treat different things as though they were the same, so we need the properties of equality. This motivates the following definition:
Definition. A relation ![]() on the set
on the set ![]() is an equivalence relation if it is reflexive, symmetric, and transitive, that is, if:
is an equivalence relation if it is reflexive, symmetric, and transitive, that is, if:
E.g. Equality is an equivalence relation.
E.g. Consider the relation ![]() on
on ![]() given by
given by ![]() iff
iff ![]() . We'll show
. We'll show ![]() is an equivalence relation.
is an equivalence relation.
Proof. First show that ![]() is reflexive. Let
is reflexive. Let ![]() be a real number. Then
be a real number. Then ![]() , so
, so ![]() .
.
Now show that ![]() is symmetric. Suppose
is symmetric. Suppose ![]() and
and ![]() are real numbers with
are real numbers with ![]() . Then
. Then ![]() , so
, so ![]() , so
, so ![]() .
.
Finally, show that ![]() is transitive. Suppose
is transitive. Suppose ![]() ,
, ![]() , and
, and ![]() are real numbers with
are real numbers with ![]() and
and ![]() . Then
. Then ![]() and
and ![]() , so
, so ![]() , i.e.
, i.e. ![]() .
. ![]()
In fact, it's easy to come up with equivalence relation on any set ![]() , given a function
, given a function ![]() : define
: define ![]() to mean
to mean ![]() .
.
E.g. Let ![]() be the relation on
be the relation on ![]() given by:
given by: ![]() iff
iff ![]() . Then
. Then ![]() is an equivalence relation.
is an equivalence relation.
E.g. Let ![]() be the relation on
be the relation on ![]() given by
given by ![]() if
if ![]() and
and ![]() have the same parity (i.e. are either both even or are both odd). Then
have the same parity (i.e. are either both even or are both odd). Then ![]() is an equivalence relation.
is an equivalence relation.
An example from algebra: modular arithmetic
The following generalizes the previous example ![]() :
:
Definition. Let ![]() be an integer. We say
be an integer. We say ![]() is equal to
is equal to ![]() modulo
modulo ![]() if
if ![]() is a multiple of
is a multiple of ![]() , i.e. if there is
, i.e. if there is ![]() with
with ![]() .
.
Theorem. Equality modulo ![]() is an equivalence relation.
is an equivalence relation.
Proof. First we'll show that equality modulo ![]() is reflexive. Let
is reflexive. Let ![]() . Then
. Then ![]() , so
, so ![]() is equal to
is equal to ![]() modulo
modulo ![]() .
.
Now we'll show that equality modulo ![]() is symmetric. Suppose
is symmetric. Suppose ![]() is equal to
is equal to ![]() modulo
modulo ![]() . Then there is some
. Then there is some ![]() with
with ![]() . So
. So ![]() , which shows that
, which shows that ![]() is a multiple of
is a multiple of ![]() , hence
, hence ![]() is equal to
is equal to ![]() modulo
modulo ![]() .
.
Now we'll show that equality modulo ![]() is transitive. Suppose
is transitive. Suppose ![]() is equal to
is equal to ![]() modulo
modulo ![]() and
and ![]() is equal to
is equal to ![]() modulo
modulo ![]() . Consider
. Consider
![]()
so ![]() is the sum of two multiples of
is the sum of two multiples of ![]() , hence a multiple of
, hence a multiple of ![]() itself. Thus
itself. Thus ![]() is equal to
is equal to ![]() modulo
modulo ![]() .
. ![]() .
.
It turns out that the arithmetic of ![]() --that is, addition, subtraction, and multiplication--makes sense if consider equality-modulo-
--that is, addition, subtraction, and multiplication--makes sense if consider equality-modulo-![]() instead of ordinary equality. We call this {\em modular arithmetic} and refer to
instead of ordinary equality. We call this {\em modular arithmetic} and refer to ![]() as the modulus.
as the modulus.
The following are standard notations for ``![]() is equal to
is equal to ![]() modulo
modulo ![]() ":
":
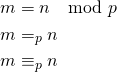
Theorem. If ![]() and
and ![]() , then
, then ![]() and
and ![]() .
.
Proof. Suppose ![]() and
and ![]() . That is, suppose
. That is, suppose ![]() and
and ![]() are multiples of
are multiples of ![]() . Then
. Then
![]()
is the sum of multiples of ![]() , hence a multiple of
, hence a multiple of ![]() . So
. So ![]() . Also
. Also
![]()
so that ![]() is the sum of two terms, each of which is a multiple of
is the sum of two terms, each of which is a multiple of ![]() , hence
, hence ![]() is a multiple of
is a multiple of ![]() , which is to say
, which is to say ![]() .
. ![]() .
.
Exercise.Show that if ![]() and
and ![]() , then
, then ![]() .
.
