You've actually dealt with modular arithmetic for most of your life: the clock face represents arithmetic with modulus 12. If you've ever served in the military or listened to the BBC World Service, you're familiar with arithmetic modulo 24 as well.
When we deal with time, we feel free to use the symbol ![]() to denote any time that is a multiple of 12 hours away from a particular 1 am or 1 pm. Notice that transitivity means we don't actually care which particular reference 1 am or 1 pm we choose -- but if you're worried about it, we could follow Bishop Ussher and say that our archetypal
to denote any time that is a multiple of 12 hours away from a particular 1 am or 1 pm. Notice that transitivity means we don't actually care which particular reference 1 am or 1 pm we choose -- but if you're worried about it, we could follow Bishop Ussher and say that our archetypal ![]() is 1 am on Sunday, 23 October 4004 BC. It is very useful to have a symbol for all of the one-o'clocks, a symbol for all of the two-o'clocks, etc., so that we can write things like
is 1 am on Sunday, 23 October 4004 BC. It is very useful to have a symbol for all of the one-o'clocks, a symbol for all of the two-o'clocks, etc., so that we can write things like
Seven hours after ![]() is
is ![]() .
.
The following definition makes this idea precise.
Definition. Let ![]() be an equivalence relation on the set
be an equivalence relation on the set ![]() , and let
, and let ![]() . The equivalence class of
. The equivalence class of ![]() under the equivalence
under the equivalence ![]() is the set
is the set
![]()
of all elements of ![]() which are equivalent to
which are equivalent to ![]() .
.
E.g. Consider the relation on ![]() given by
given by ![]() if
if ![]() . Then
. Then ![]() ,
, ![]() , etc.
, etc.
E.g. Consider the equivalence relation ![]() on
on ![]() given by
given by ![]() if
if ![]() . Then
. Then
![Rendered by QuickLaTeX.com \begin{align*} [(0,0)]_C&=\left\{(z,w)\middle|z^2+w^2=0\right\}=\{(0,0)\}\\ [(0,1)]_C&=\left\{(z,w)\middle|z^2+w^2=1\right\}\\ &=\text{circle of radius }1\text{ at the origin}\\ [(1,1)]_C&=\left\{(z,w)\middle|z^2+w^2=2\right\}\\ &=\text{circle of radius }\sqrt{2}\text{ at the origin} \end{align*}](https://ma225.wordpress.ncsu.edu/wp-content/ql-cache/quicklatex.com-42436c40edeb47e9eca9f78ada178699_l3.png)
and it's easy to see that all other equivalence classes will be circles centered at the origin. Note that we have ![]() .
.
Definition. Given an equivalence relation ![]() on
on ![]() , the set of all equivalence classes is called the {\em quotient of
, the set of all equivalence classes is called the {\em quotient of ![]() by
by ![]() }. We write
}. We write
![]()
Notice that the quotient of ![]() by an equivalence relation is a set of sets of elements of
by an equivalence relation is a set of sets of elements of ![]() .
.
E.g. Consider the relation on ![]() given by
given by ![]() if
if ![]() . Then
. Then ![]()
E.g. If ![]() is the equivalence relation on
is the equivalence relation on ![]() given by
given by ![]() if
if ![]() , then
, then ![]() is the set of circles centered at the origin.
is the set of circles centered at the origin.
E.g. ![]() has 12 elements:
has 12 elements:
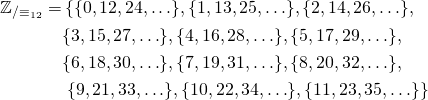
A convenient way to represent them is ![]() ,
, ![]() ,
, ![]() , etc. Notice that the mathematical convention is to start at 0 and go up to 11, which is different from how clocks are numbered.
, etc. Notice that the mathematical convention is to start at 0 and go up to 11, which is different from how clocks are numbered.
Theorem. Let ![]() be an equivalence relation on
be an equivalence relation on ![]() . Let
. Let ![]() .
. ![]() iff
iff ![]() .
.
Proof. Suppose ![]() . Since
. Since ![]() , we have
, we have ![]() , so by definition of
, so by definition of ![]() , we have
, we have ![]() .
.
Suppose ![]() . We'll show
. We'll show ![]() . Let
. Let ![]() . Then
. Then ![]() . Since
. Since ![]() is transitive, we have
is transitive, we have ![]() . Since
. Since ![]() is symmetric, this means
is symmetric, this means ![]() , i.e.
, i.e. ![]() .
.
The proof that ![]() is similar.
is similar. ![]() .
.
Theorem. ![]() consists of exactly the elements
consists of exactly the elements ![]() ,
, ![]() , \ldots,
, \ldots, ![]() .
.
Proof. We are asked to show set equality. It is clear that each ![]() for
for ![]() is an equivalence class, so we have one set inclusion.
is an equivalence class, so we have one set inclusion.
To get the other set inclusion, suppose ![]() is an equivalence class. Then there is some
is an equivalence class. Then there is some ![]() with
with ![]() . We apply the Division Algorithm to write
. We apply the Division Algorithm to write
![]()
where ![]() . Then
. Then ![]() is a multiple of
is a multiple of ![]() , so
, so ![]() . Thus
. Thus ![]() , and since
, and since ![]() , we have shown that
, we have shown that ![]() is on our list of equivalence classes.
is on our list of equivalence classes. ![]() .
.
An important property of equivalence classes is they ``cut up" the underlying set:
Theorem. Let ![]() be a set and
be a set and ![]() be an equivalence relation on
be an equivalence relation on ![]() . Then:
. Then:
- No equivalence class is empty.
- The equivalence classes cover
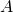 ; that is,
; that is, ![Rendered by QuickLaTeX.com A\subseteq \displaystyle\bigcup_{a\in A}[a]_R](https://ma225.wordpress.ncsu.edu/wp-content/ql-cache/quicklatex.com-2bc0cb33db7c0f965393058afd3d2663_l3.png) .
. - Equivalence classes do not overlap.
Proof. The first two are fairly straightforward from reflexivity.
- Any equivalence class is
![Rendered by QuickLaTeX.com [x]_R](https://ma225.wordpress.ncsu.edu/wp-content/ql-cache/quicklatex.com-8c099de9c23f54de49a2bae9a64d6d3d_l3.png) for some
for some 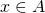 . Since
. Since 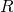 is reflexive,
is reflexive, 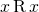 , i.e.
, i.e. ![Rendered by QuickLaTeX.com x\in[x]_R](https://ma225.wordpress.ncsu.edu/wp-content/ql-cache/quicklatex.com-8a6bccd9ef6a2f6613d4ad69deb86ff7_l3.png) . So
. So ![Rendered by QuickLaTeX.com [x]_R](https://ma225.wordpress.ncsu.edu/wp-content/ql-cache/quicklatex.com-8c099de9c23f54de49a2bae9a64d6d3d_l3.png) is nonempty.
is nonempty. - Let
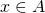 . We need to show that
. We need to show that ![Rendered by QuickLaTeX.com x\in\displaystyle\bigcup_{a\in A}[a]_R](https://ma225.wordpress.ncsu.edu/wp-content/ql-cache/quicklatex.com-b69afd83640dffd651ec0d58e2c44570_l3.png) . That is, we need to find some
. That is, we need to find some 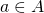 for which
for which ![Rendered by QuickLaTeX.com x\in[a]_R](https://ma225.wordpress.ncsu.edu/wp-content/ql-cache/quicklatex.com-fb1cb9dfabe2342e5d6bfe644b9e3993_l3.png) . Using
. Using 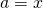 and the observation above, we have
and the observation above, we have ![Rendered by QuickLaTeX.com x\in[x]_R](https://ma225.wordpress.ncsu.edu/wp-content/ql-cache/quicklatex.com-8a6bccd9ef6a2f6613d4ad69deb86ff7_l3.png) .
.
The third clause is trickier, mostly because we need to understand what it means. Consider the case of ![]() ,
, ![]() . Then
. Then ![]() and
and ![]() certainly overlap--they both contain
certainly overlap--they both contain ![]() , for example. So if we take ``equivalence classes do not overlap" too literally it cannot be true.
, for example. So if we take ``equivalence classes do not overlap" too literally it cannot be true.
But notice that ![]() and
and ![]() not only overlap, but in fact are equal. So we'll amend
not only overlap, but in fact are equal. So we'll amend
equivalence classes do not overlap
to
distinct equivalence classes do not overlap
that is,
Theorem. If ![]() then
then ![]() .
.
Proof. We'll prove the contrapositive: if ![]() , then
, then ![]() .
.
Assume ![]() is nonempty. Then there is some
is nonempty. Then there is some ![]() . So
. So ![]() and
and ![]() .
.
Since ![]() is symmetric,
is symmetric, ![]() .
.
Since ![]() is transitive,
is transitive, ![]() . So
. So ![]() .
. ![]() .
.
This theorem shows, for example, that there are in no redundancies on the list ![]() ,
, ![]() , \ldots,
, \ldots, ![]() of equivalence classes modulo
of equivalence classes modulo ![]() .
.
An example from arithmetic: rational numbers
Exercise. Consider the relation on ![]() given by:
given by: ![]() if
if ![]() . Show that
. Show that ![]() is an equivalence relation. Do not use fractions in your proof.
is an equivalence relation. Do not use fractions in your proof.
What are the equivalence classes under the relation ![]() ?
?
Claim. ![]() is the set of all pairs of the form
is the set of all pairs of the form ![]() .
.
Proof. First we show that every ![]() . This is equivalent to showing
. This is equivalent to showing ![]() . But by definition of
. But by definition of ![]() , all we need to show is
, all we need to show is ![]() --which is clear since both sides are
--which is clear since both sides are ![]() .
.
Now we show that if ![]() , then it must be the case that
, then it must be the case that ![]() .
. ![]() means that
means that ![]() , i.e. that
, i.e. that ![]() .
. ![]() .
.
Exercise. Show that ![]() is the set of all pairs of the form
is the set of all pairs of the form ![]() .
.
We write ![]() for the equivalence class
for the equivalence class ![]() , and we define:
, and we define:
Definition. The set of rational numbers ![]() is
is ![]() . That is, a rational number is an equivalence class of pairs of integers.
. That is, a rational number is an equivalence class of pairs of integers.
