There are two ways to think about drawing a picture of a relation on a set ![]() .
.
if 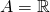
We can draw relations on ![]() , because they are subsets of
, because they are subsets of ![]() -- i.e., subsets of the plane. Actually you've been drawing these pictures since way back.
-- i.e., subsets of the plane. Actually you've been drawing these pictures since way back.
For example, let's consider the relation ![]() given by
given by ![]() if
if ![]() . The picture looks like:
. The picture looks like:
Here I've put ![]() in blue, and its complement
in blue, and its complement ![]() in red.
in red.
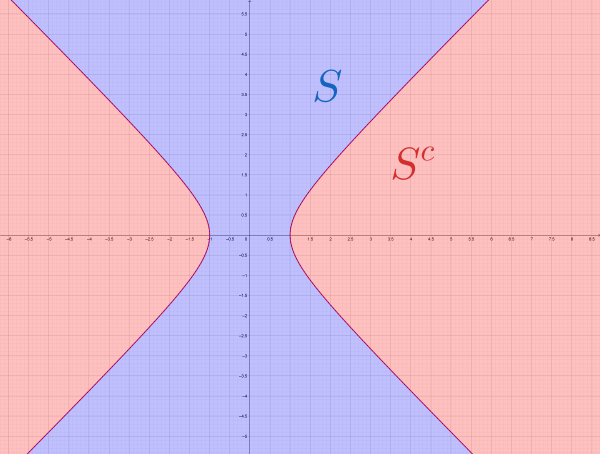
What does ![]() look like?
look like? ![]() means
means ![]() , i.e.
, i.e. ![]() . Here's that, in green.
. Here's that, in green.
Notice that ![]() and
and ![]() are general rather different things (that's as we saw before).
are general rather different things (that's as we saw before).
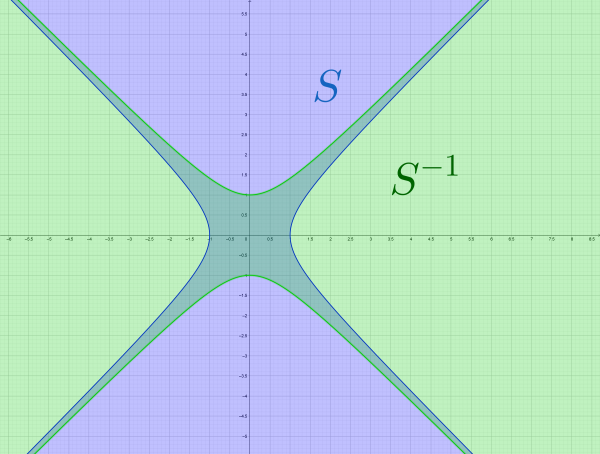
To get ![]() from
from ![]() , we swap the roles of
, we swap the roles of ![]() and
and ![]() . visually, this looks like reflection across the line
. visually, this looks like reflection across the line ![]() . Here's another example, with the line
. Here's another example, with the line ![]() draw on explicitly:
draw on explicitly:
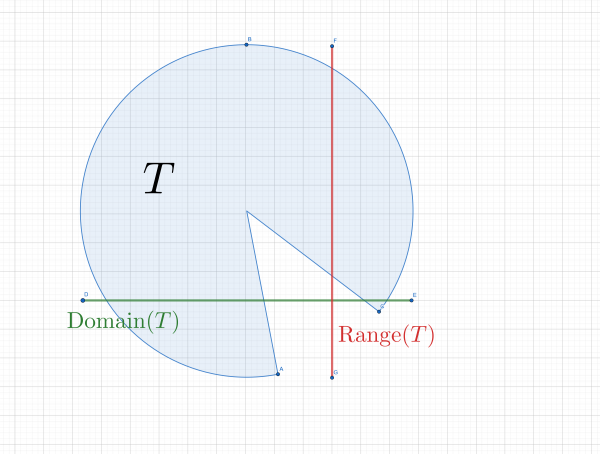
We can use such a visual depiction to compute the domain and range of a relation: the domain is the "horizontal shadow" and the range is the "vertical shadow:
We can also use such a depiction to check some properties of relations. For example: for ![]() to be reflexive on
to be reflexive on ![]() means every
means every ![]() has
has ![]() . That is, every pair
. That is, every pair ![]() . All of the pairs of the form
. All of the pairs of the form ![]() constitute the diagonal line
constitute the diagonal line ![]() . Thus we can check reflexivity by asking: does the relation contain the diagonal line?
. Thus we can check reflexivity by asking: does the relation contain the diagonal line?
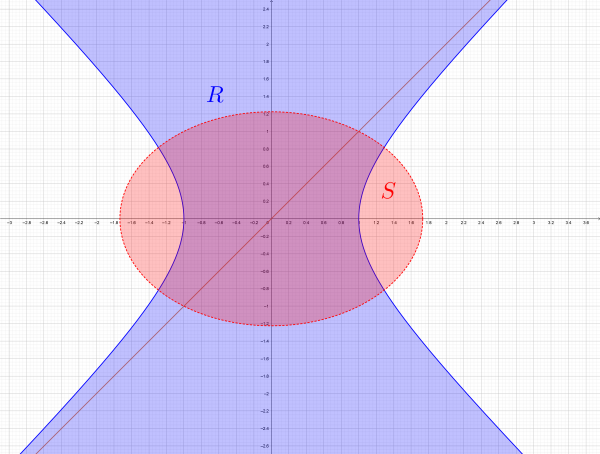
Here the relation ![]() is reflexive --- it contains the line
is reflexive --- it contains the line ![]() --- and the relation
--- and the relation ![]() is not.
is not.
We can also check symmetry. For ![]() to be symmetric means
to be symmetric means ![]() guarantees
guarantees ![]() . That is, if we reflect
. That is, if we reflect ![]() across the line
across the line ![]() , we should land in in
, we should land in in ![]() again. That is,
again. That is, ![]() being symmetric means
being symmetric means ![]() is symmetric about the line
is symmetric about the line ![]() . Neither
. Neither ![]() nor
nor ![]() above is symmetric.
above is symmetric.
Transitivity is a bit more fun to check. Transitivity is relevant to pairs ![]() and
and ![]() both in
both in ![]() . Here we'll check whether
. Here we'll check whether ![]() , given by
, given by ![]() if
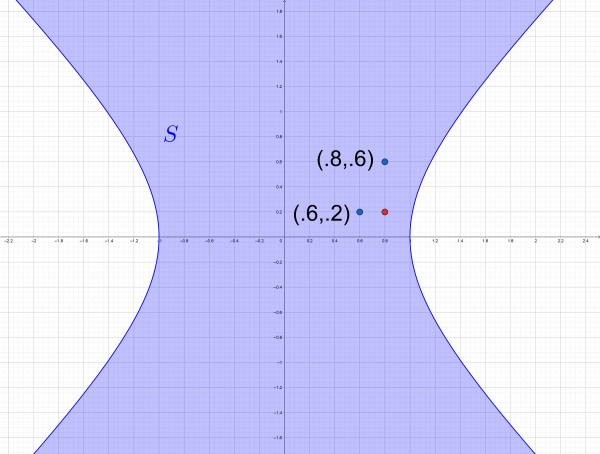
if ![]() , is transitive. We have
, is transitive. We have ![]() and
and ![]() , so we check to see if
, so we check to see if ![]() . Here,
. Here, ![]() is indicated in red --- it's in
is indicated in red --- it's in ![]() . But we need this to hold for every such pair of points in
. But we need this to hold for every such pair of points in ![]() .
.
Unfortunately, it does not:
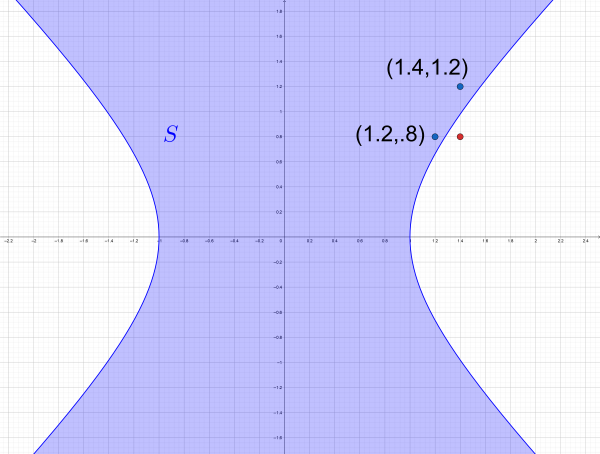
It's a bit hard to see visually just what transitivity means, but you can see that it's got something to do with right triangles.
if 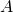 is a finite set
is a finite set
If ![]() is a finite set, we can draw what's called a directed graph, or digraph, of the relation
is a finite set, we can draw what's called a directed graph, or digraph, of the relation ![]() . A directed graph is a collection of vertices, which we draw as points, and directed edges, which we draw as arrows between the points. For example, let's take the set
. A directed graph is a collection of vertices, which we draw as points, and directed edges, which we draw as arrows between the points. For example, let's take the set ![]() and the relation
and the relation ![]() if
if ![]() .
.
The digraph corresponding to this relation is draw like this: we know ![]() ,
, ![]() , and
, and ![]() . So we draw three arrows starting from 2. We also know that
. So we draw three arrows starting from 2. We also know that ![]() and
and ![]() , so we draw those:
, so we draw those:
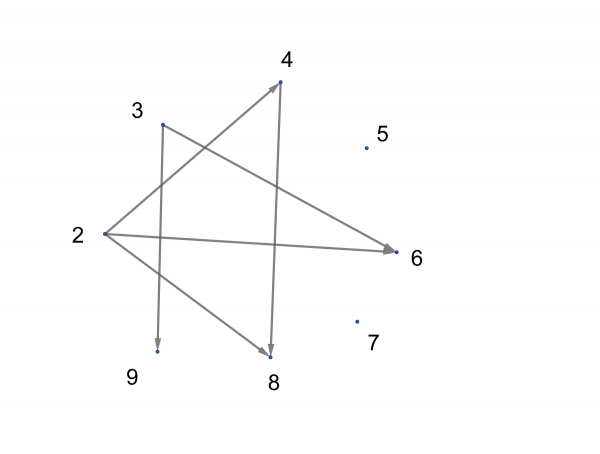
But that's not all. We also know that ![]() , for example. So we need to add arrows that start and end at each vertex:
, for example. So we need to add arrows that start and end at each vertex:
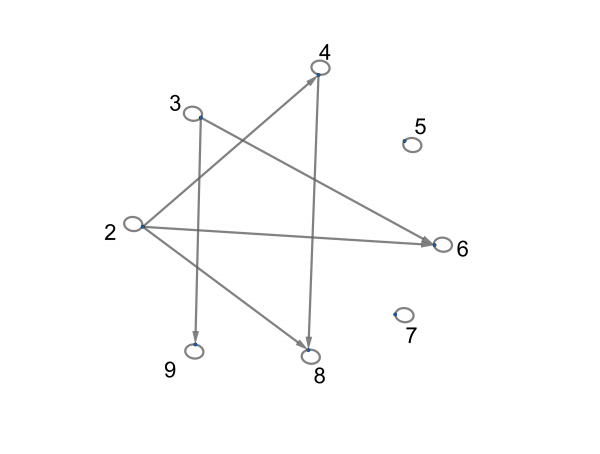
Observe that divides, as a relation on this set, is transitive: whenever we have ![]() and
and ![]() , we automatically have
, we automatically have ![]() . We can recognize this in the digraph by checking that, whenever there are two arrows connected head to tail, the third leg of that triangle is present:
. We can recognize this in the digraph by checking that, whenever there are two arrows connected head to tail, the third leg of that triangle is present:
 Exercise. What do symmetry and reflexivity look like in the digraph?
Exercise. What do symmetry and reflexivity look like in the digraph?
