Assumptions are the termites of relationships.
character of Arthur Fonzarelli, Happy Days
Now we are ready to consider some properties of relations. Our interest is to find properties of, e.g. motherhood. To do this, remember that we are not interested in a particular mother or a particular child, or even in a particular mother-child pair, but rather motherhood in general.
We'll start with properties that make sense for relations whose source and target are the same, that is, relations on a set.
Definition. Let ![]() be a relation on the set
be a relation on the set ![]() .
.
- We call
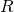 reflexive if every element of
reflexive if every element of 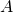 is related to itself; that is, if every
is related to itself; that is, if every 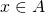 has
has 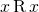 .
. - We call
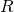 irreflexive if no element of
irreflexive if no element of 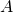 is related to itself.
is related to itself. - We call
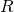 symmetric if
symmetric if 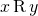 means the same thing as
means the same thing as 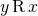 .
. - We call
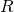 asymmetric if
asymmetric if 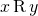 guarantees that
guarantees that 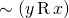 .
. - We call
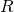 antisymmetric if the only way for
antisymmetric if the only way for 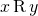 and
and 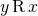 to both be true is if
to both be true is if 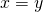 .
. - We call
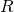 transitive if
transitive if 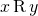 and
and 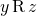 together guarantee
together guarantee 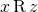 .
.
Exercise. Explain why none of these relations makes sense unless the source and target of ![]() are the same set.
are the same set.
Exercise. Which of the above properties does the motherhood relation ![]() have?
have?
Exercise. Write the definitions above using set notation instead of infix notation.
Exercise. Write the definitions of reflexive, symmetric, and transitive using logical symbols.
Checking whether a given relation has the properties above looks like:
E.g. `Divides' (as a relation on the integers) is reflexive and transitive, but none of: symmetric, asymmetric, antisymmetric.
Proof. We'll show reflexivity first. Suppose ![]() is an integer. Then
is an integer. Then ![]() , so
, so ![]() divides
divides ![]() .
.
Now we'll show transitivity. Suppose ![]() divides
divides ![]() and
and ![]() divides
divides ![]() . Then there are
. Then there are ![]() and
and ![]() so that
so that ![]() and
and ![]() . Then
. Then ![]() , so
, so ![]() divides
divides ![]() .
.
Note that 2 divides 4 but 4 does not divide 2. This counterexample shows that `divides' is not symmetric.
Note that 4 divides 4. This counterexample shows that `divides' is not asymmetric.
Note that ![]() divides
divides ![]() and
and ![]() divides
divides ![]() , but
, but ![]() . This counterexample shows that `divides' is not antisymmetric.
. This counterexample shows that `divides' is not antisymmetric. ![]()
E.g. ![]() is irreflexive, asymmetric, transitive, and antisymmetric, but neither reflexive nor symmetric.
is irreflexive, asymmetric, transitive, and antisymmetric, but neither reflexive nor symmetric.
Exercise. Show that `divides' as a relation on ![]() is antisymmetric.
is antisymmetric.
