Besides the ordinary set operations, there are special operations we can perform on relations.
Definition. The inverse of a relation ![]() from
from ![]() to
to ![]() is the relation from
is the relation from ![]() to
to ![]() defined by:
defined by:
![]()
That is, ![]() iff
iff ![]() iff
iff ![]() iff
iff ![]() .
.
E.g. ![]() iff
iff ![]() iff
iff ![]() .
.
That is, the inverse of the less-than relation is the greater-than relation.
Note that the inverse and the complement are very different things, because the complement of less-than is greater-than-or-equal-to.
Exercise. What is the inverse of the identity relation?
Definition. If ![]() is a relation from
is a relation from ![]() to
to ![]() and
and ![]() is a relation from
is a relation from ![]() to
to ![]() , we define the {\em composite relation}
, we define the {\em composite relation} ![]() from
from ![]() to
to ![]() by:
by:
![]()
Note that the source of ![]() is the source of
is the source of ![]() and the target of
and the target of ![]() is the target of
is the target of ![]() .
.
We can think of ![]() as a stepping stone between
as a stepping stone between ![]() and
and ![]() .
. ![]() consists of all the pairs
consists of all the pairs ![]() such that there is such a stepping stone, as we pass from the source of
such that there is such a stepping stone, as we pass from the source of ![]() to the target of
to the target of ![]() .
.
Observe that unless the target of ![]() and the source of
and the source of ![]() are the same, we can't even make sense of
are the same, we can't even make sense of ![]() . So most composites aren't defined, and we must first check that two relations are compatible before we try to compose them. Even if
. So most composites aren't defined, and we must first check that two relations are compatible before we try to compose them. Even if ![]() is defined,
is defined, ![]() usually isn't.
usually isn't.
In lower mathematics courses, you probably only encountered relations on ![]() , so that all sources and targets were the same---thus, all compositions were defined. The sole exception to this is in multivariable calculus. This is precisely why the multivariable Chain Rule is so much more complicated than its single-variable counterpart.
, so that all sources and targets were the same---thus, all compositions were defined. The sole exception to this is in multivariable calculus. This is precisely why the multivariable Chain Rule is so much more complicated than its single-variable counterpart.
Exercise. Formulate the definition of ![]() in infix notation. That is, explain what
in infix notation. That is, explain what ![]() means.
means.
Exercise. Consider the set ![]() of all people, and the relations
of all people, and the relations ![]() and
and ![]() on
on ![]() given by:
given by: ![]() iff
iff ![]() is
is ![]() 's mother and
's mother and ![]() iff
iff ![]() is
is ![]() 's father. Explain what the following relations mean:
's father. Explain what the following relations mean: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Theorem. Let ![]() be a relation from
be a relation from ![]() to
to ![]() ,
, ![]() a relation from
a relation from ![]() to
to ![]() , and
, and ![]() a relation from
a relation from ![]() to
to ![]() . Then
. Then
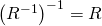
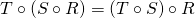
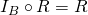 and
and 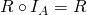
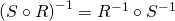
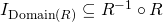 and
and 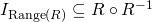 .
.
Proof. We'll prove the last clause, and leave the others as exercises.
Since we need to prove ![]() , let
, let ![]() . Then
. Then ![]() for some
for some ![]() . Since
. Since ![]() , there is some
, there is some ![]() with
with ![]() . So
. So ![]() . So
. So ![]() .
.
To show ![]() , let
, let ![]() . Then
. Then ![]() for some
for some ![]() . Since
. Since ![]() , there is some
, there is some ![]() with
with ![]() . Then
. Then ![]() . So
. So ![]() .
.
