Let's get another little word.
Definition. Given two propositions ![]() and
and ![]() , the proposition
, the proposition ![]() (read
(read ![]() or
or ![]() ) has truth value as given below:
) has truth value as given below:
| T | T | T | 1 |
| T | F | T | 2 |
| F | T | T | 3 |
| F | F | F | 4 |
Exercise. Prove the following propositions. First make sure you know what they mean.
Proposition. ![]() is commutative.
is commutative.
Proposition. ![]() is associative.
is associative.
Lines 2-4 probably aren't surprising, but line 1 bothers pretty much everybody, so we should explore it a bit. Consider a statement like Barack Obama was born in Hawaii or Angela Merkel has a Ph.D. in chemistry. The two statements that make up this statement are both true (Obama was indeed born in Hawaii, and Merkel was a chemist before entering politics), so this is the type of statement that's relevant to line 1. But we normally wouldn't use the word or here; we'd use the word and instead. So seeing it written with the word or kind of makes us uncomfortable. Unfortunately (actually, very fortunately) there isn't the option to assign a truth value of U -- we have to give either a T or an F. And (there's a long story, which you'll work out for homework) it turns out to be much better to give a T than to give an F.
When we want to be extra clear, we refer to this flavor of or -- the one with a T in the first row -- we call it inclusive or. Generally speaking mathematicians use inclusive or, so get used to it!
Let's take a look at how ![]() interacts with
interacts with ![]() . Try your hand at proving the following, using truth tables:
. Try your hand at proving the following, using truth tables:
Theorem. ![]() and
and ![]() distribute over one another; that is:
distribute over one another; that is:
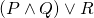 is equivalent to
is equivalent to 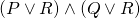 (this is
(this is  distributing over
distributing over  .)
.)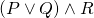 is equivalent to
is equivalent to 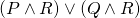 (this is
(this is  distributing over
distributing over  .)
.)
We also have the following very useful and very interesting result, which lets us translate between ands and ors:
De Morgan's Law:
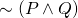 is equivalent to
is equivalent to 
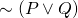 is equivalent to
is equivalent to 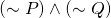
Augustus de Morgan, British, 1806-1871, got his name attached to this result because he formulated much of the modern notation we use for logic. But he didn't invent or discover it -- it's better to call him an annotated translator of classical Indian sources.
We are now ready to give our first logical computation, and formulate a useful denial of ![]() . We'll use the symbol
. We'll use the symbol ![]() to mean is equivalent to.
to mean is equivalent to.
![Rendered by QuickLaTeX.com \begin{equation*}\begin{aligned} &\sim\left[(P\wedge Q)\vee R\right]\\ &\equiv \left(\sim(P\wedge Q)\right)\wedge (\sim R)&\text{De Morgan's Law 2}\\ &\equiv \left((\sim P)\vee (\sim Q)\right)\wedge (\sim R)&\text{De Morgan's Law 1} \end{aligned}\end{equation*}](https://ma225.wordpress.ncsu.edu/wp-content/ql-cache/quicklatex.com-37a77a713433e47098be0a4b935b1c3b_l3.png)
Notice that just as in arithmetic, we work from the outside in, and write each step out. Also just as with arithmetic (and this can't be emphasized enough) brackets are both useful and necessary!
The formula we ended with looks very little like the formula we started with--for example, it's much longer. Why might a formula like
![]()
be more useful than
![]()
Let's assign the variables as follows:

Then ![]() says
says
Either roses are red and violets are blue, or the king of France is bald.
Its denial ![]() says
says
It is not the case that either roses are red and violets are blue, or the king of France is bald.
But what does that mean? Our logical computation says that it means just the same thing as
The king of France is not bald, and either roses aren't red or violets aren't blue.
Try convincing yourself, and explaining to someone else, why these two denials mean the same thing.
As with arithmetic, this is not the only way to come up with a denial of ![]() . Above we applied de Morgan's Law first; but since we know that
. Above we applied de Morgan's Law first; but since we know that ![]() and
and ![]() distribute over one another, we could equally well have derived
distribute over one another, we could equally well have derived
![Rendered by QuickLaTeX.com \begin{equation*} \begin{aligned} &\sim\left[(P\wedge Q)\vee R\right]\\ &\equiv \sim\left[R\vee(P\wedge Q)\right]\\ &\equiv \sim\left[(R\vee P)\wedge (R\vee Q)\right]\\ &\equiv \left[\sim(R\vee P)\right]\vee\left[\sim(R\vee Q)\right]&\text{de Morgan's Law 1}\\ &\equiv \left[(\sim R)\wedge (\sim P)\right]\vee\left[(\sim R)\wedge(\sim Q)\right]&\text{de Morgan's Law 2} \end{aligned} \end{equation*}](https://ma225.wordpress.ncsu.edu/wp-content/ql-cache/quicklatex.com-ee30c115adb055aa32145dc4641f600a_l3.png)
which reads Either the king of France is not bald and roses are not red, or the king of France is not bald and violets are not blue.
As with arithmetic, the commutative, associative, and distributive rules for ![]() and
and ![]() will become so second nature to you that will begin applying them without thinking about it. But here we've spelled everything out.
will become so second nature to you that will begin applying them without thinking about it. But here we've spelled everything out.
