All in all, those who were chained would consider nothing besides the shadows of the artifacts.
Plato, The Allegory of the Cave
Pushforwards and Pullbacks
A function ![]() gives us a way of taking elements in
gives us a way of taking elements in ![]() and pushing them over to
and pushing them over to ![]() . We call
. We call ![]() the image of
the image of ![]() under
under ![]() . In fact, we can also think of
. In fact, we can also think of ![]() as giving a way to push a set of elements of
as giving a way to push a set of elements of ![]() over to
over to ![]() .
.
Definition. Given ![]() and
and ![]() , we define
, we define ![]() . We call
. We call ![]() the image of
the image of ![]() under
under ![]() or the pushforward of
or the pushforward of ![]() by
by ![]() .
.
Notice that by definition, ![]() is a subset of the target
is a subset of the target ![]() .
.
E.g. If ![]() , and
, and ![]() , then
, then ![]() .
.
Proof. (![]() ) Let
) Let ![]() . Then
. Then ![]() . So
. So ![]() .
.
If ![]() , then
, then ![]() is between
is between ![]() and
and ![]() . So
. So ![]() .
.
If ![]() , then
, then ![]() is between
is between ![]() and
and ![]() . So
. So ![]() .
.
(![]() ) Let
) Let ![]() . Then
. Then ![]() . Let
. Let ![]() . So
. So ![]() . Then
. Then ![]() . Since
. Since ![]() ,
, ![]() .
.
Notation. Most sources write ![]() for the image of
for the image of ![]() under
under ![]() . This is not an entirely unreasonable choice, but it means that the symbol
. This is not an entirely unreasonable choice, but it means that the symbol ![]() has two interpretations -- if
has two interpretations -- if ![]() is an element of
is an element of ![]() , then
, then ![]() is an element of
is an element of ![]() ; if
; if ![]() is a subset of
is a subset of ![]() , then
, then ![]() is a subset of
is a subset of ![]() . Our notation
. Our notation ![]() is always going to be a set. But you should know, for your future mathematics courses, that
is always going to be a set. But you should know, for your future mathematics courses, that ![]() is a standard notation.
is a standard notation.
Theorem/Realization. If ![]() , then
, then ![]() .
.
That is, ![]() takes subsets of
takes subsets of ![]() and yields subsets of
and yields subsets of ![]() .
.
Definition. Given ![]() and
and ![]() , we define
, we define ![]() . We call
. We call ![]() the preimage of
the preimage of ![]() under
under ![]() or the pullback of
or the pullback of ![]() by
by ![]() .
.
Note that ![]() is a subset of the domain
is a subset of the domain ![]() .
.
E.g. If ![]() is given by
is given by ![]() , then
, then ![]() and
and ![]() .
.
Theorem/Realization. If ![]() , then
, then ![]() .
.
Notation. Just like with the image, there is a standard-but-terrible notation for the preimage. Most sources write ![]() for the preimage of
for the preimage of ![]() under
under ![]() . This is just nutty, because the object in question doesn't have anything to do with inverses. Nevertheless, you should expect at least once in your mathematical life to have to deal with the string of symbols
. This is just nutty, because the object in question doesn't have anything to do with inverses. Nevertheless, you should expect at least once in your mathematical life to have to deal with the string of symbols ![]() , where
, where ![]() is some set. We live in a fallen world.
is some set. We live in a fallen world.
Theorem. Let ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Then
. Then
Proof. This is an exercise, but it's just an exercise in proving set equalities.
Characteristic Functions
Recall that for ![]() to be a set means that ``
to be a set means that ``![]() " is an open sentence. We can view this in terms of functions.
" is an open sentence. We can view this in terms of functions.
Definition. Given a set ![]() , the characteristic function of
, the characteristic function of ![]() is the function
is the function
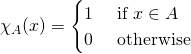
Technically in order to define this function, we need to specify a universe for ![]() -- but notice that it really doesn't much matter, because as long as
-- but notice that it really doesn't much matter, because as long as ![]() ,
, ![]() .
.
Exercise. If ![]() and
and ![]() are subsets of some common universe
are subsets of some common universe ![]() , then for any
, then for any ![]() , we have:
, we have:
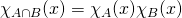 ,
,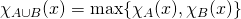
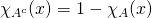 .
.
Theorem. ![]() .
.
This says that ![]() determines its characteristic function, and
determines its characteristic function, and ![]() determines
determines ![]() as well.
as well.
