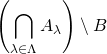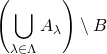Finite Set Operations
The operations ![]() and
and ![]() apply to two sets; we can however use them to combine more than one set. If we have a finite collection of sets
apply to two sets; we can however use them to combine more than one set. If we have a finite collection of sets ![]() , we write
, we write
(1) 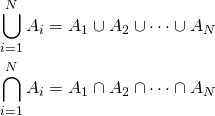
Activity. Give a better definition of ![]() and
and ![]() . (Hint. What did we say about definitions involving
. (Hint. What did we say about definitions involving ![]() ?)
?)
De Morgan's Laws. For any finite collection of sets ![]() ,
,
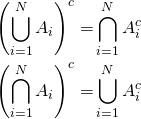
Exercise. Prove this version of de Morgan's Laws.
Transfinite Operations
There is no reason to restrict our attention to {\em finite} collections of sets. For example, we might consider
the collection of intervals of the form ![]() , where
, where ![]() is allowed to be an natural number,
is allowed to be an natural number,
or perhaps
the set of all disks centered at the origin
each of which consists of an infinite number of sets. We usually use set-builder notation to write something like
(2) ![]()
or
(3) ![]()
to emphasize that what we are dealing with is a(n infinite) set of sets. (Here we have written ![]() for the disk of radius
for the disk of radius ![]() centered at the origin.) We call the set to the right of the pipe the index set: in these collections the index sets are
centered at the origin.) We call the set to the right of the pipe the index set: in these collections the index sets are ![]() and the interval
and the interval ![]() , respectively.
, respectively.
We can define unions and intersections of such infinite collections of sets by recalling that ![]() acts like a souped-up version of
acts like a souped-up version of ![]() and
and ![]() acts like a souped-up version of
acts like a souped-up version of ![]() .
.
Given a collection of sets ![]() , we set
, we set
Definition.
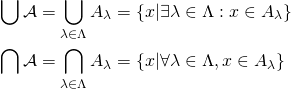
E.g. ![]()
Proof. Let ![]() . Then there is some
. Then there is some ![]() with
with ![]() , so
, so ![]() . Thus
. Thus ![]() .
.
Now let ![]() . Then there is some
. Then there is some ![]() with
with ![]() . But
. But ![]() , so
, so ![]() .
. ![]()
E.g. ![]()
Proof. Certainly the origin ![]() is in each disk
is in each disk ![]() . We will show it is the only such point.
. We will show it is the only such point.
Consider any point ![]() in the plane. Let
in the plane. Let ![]() be the distance between
be the distance between ![]() and the origin. Then if we select
and the origin. Then if we select ![]() , we see that
, we see that ![]() . Thus
. Thus ![]() cannot be in every
cannot be in every ![]() .
.
de Morgan's Laws. For any collection ![]() , we have
, we have
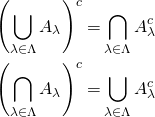
Exercise. Prove this version of de Morgan's Laws.
Exercise. What is each of the following sets?
Exercise Express each set below as either a generalized union or a generalized intersection, and also express it in set-builder notation.