Set-Builder Notation – Foundations of Mathematics

Recall that, by definition, $S$ being a set is equivalent to `` $x\in S$ " being an open sentence. This means that the theory of sets and the theory of logic are basically the same--differing only by notation and perspective. One can exploit this correspondence by using open sentences to define sets. Given an open sentence $P(t)$ , we can define the corresponding set $S_P$ , which consists of all values $t$ so that $P(t)$ is true. We write

$S_P=\left\{t\middle\vert P(t)\right\}$

and read aloud `` $S_P$ is the set of all $t$ such that $P(t)$ ." In other words, $S_P$ is the set so that $x\in S_P$ means exactly $P(x)$ . This way of defining sets has the unfortunately puerile name set-builder notation. It's how most sets in most mathematics texts are defined. By way of example, we'll rephrase some previous definitions.

Definition.

$A^c=\left\{x\middle\vert x\notin A\right\}$
$A\cup B= \left\{p\middle\vert p\in A\vee p\in B\right\}$

Activity Complete the list of set operations by giving set-builder descriptions of each of the following set operations.

$A\cap B$
$A\setminus B$
$\left(A\setminus B\right)\cup\left(B\setminus A\right)$
$2^B$

Exercise. Consider two sets, $A=\left\{x\middle\vert P(x)\right\}$ and $B=\left\{t\middle\vert Q(t)\right\}$ . What can we say about the open sentences $P$ and $Q$ if we know each of the following facts about the sets $A$ and $B$ ?

$A=B$
$A\subseteq B$
$A=\varnothing$
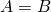
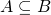
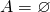
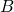$B$ is the universe

The last exercise referenced the universe, which naturally leads to the question of how to specify the universe in set-builder notation. An even number is an integer which is twice some other integer. So we could write

Definition.

*** QuickLaTeX cannot compile formula:
\begin{equation*}\left\{n\middle\vert n\in\mathbb{Z}\wedge\exists k:\left(k\in \mathbb{Z}\wedge n=2k\right) \right\}
But the right-hand side (after the pipe symbol $\vert$) is a little crowded. Doing the same trick as we did in, we want to handle the conditions $n\in\mathbb{Z}$ and $k\in\mathbb{Z}$ by changing the universe. We do this as follows:
<strong>Definition. </strong>The set of even numbers is the set \begin{equation*}\left\{n\in\mathbb{Z}\middle\vert \exists k\in\mathbb{Z}:n=2k\right\}\end{equation*}

*** Error message:
Display math should end with $$.
leading text: ...ht-hand side (after the pipe symbol $\vert

We would read this aloud ``The set of all integers $n$ such that there is an integer $k$ with $n=2k$ ." In this version of set-builder notation, the left-hand side (before the pipe) is about what kind of objects the elements of the set being defined are; the right-hand side gives a condition that describes the set.

There is yet another way to use set-builder notation to define a set, as exemplified:

Definition.

$\begin{equation*} \left\{2k\middle\vert k\in\mathbb{Z}\right\} \end{equation*}$

We would read this aloud ``The set of a numbers of the form $2k$ , where $k$ is an integer." Notice that $n$ has disappeared entirely from this version. In this version of set-builder notation, the left-hand side gives the general form of the elements of the set, and the right-hand side tells us which elements of that form actually occur in the set.

Where are the quantifiers?

Learning to let go of your 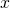$x$ s

An open sentence like

$E(x):\ \ \ \exists k: x=2k$

has two variables and one quantifier. The two variables are used in quite different ways. First, notice that the only variable that's eligible for plugging in to $E$ is $x$ : we can sensibly ask Is it true that $E(2)$ ? and Is it true that $E(3)$ ?. But substituting for $k$ like this:

$\exists 7: x=2\cdot 7$

yields nonsense.

What's going on here? Variables where we can plug in values and get something sensible (like $x$ here) are called free. The other kind of variable (like $k$ here) is called a bound variable, from the verb bind. The idea is that the quantifier $\exists$ has a binding effect on the variable. You can recognize bound variables in three ways:

Substituting for a bound variable results in nonsense; substituting for a free variable does not.
Bound variables almost always occur exactly twice; free variables occur once.
There is always a way to read a mathematical formula containing a bound variable in a way that makes the bound variable go away.

I'll illustrate these checks by giving some examples of bound variables, one of which you've seen before:

Consider the integral

$\int_a^b x^2\ dx$

The variables $a$ and $b$ are free; the variable $x$ is bound.

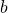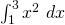We could substitute in for $a$ and $b$ : $\int_1^3x^2\ dx$ . If we substitute for 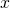$x$ , we get 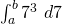$\int_a^b 7^3\ d7$ , which is nonsense.
The variable 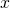$x$ occurs twice: once in the integrand and once in the differential.
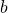We could read this integral aloud as ``The integral, from $a$ to $b$ , of the squaring function."

Consider the (true) statement

$\forall x, x^2<9 \Rightarrow x^3<27$

Here, the variable $x$ is bound and there are no free variables.

If we tried to substitute, we'd get something like 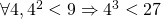$\forall 4, 4^2<9 \Rightarrow 4^3<27$ , which doesn't make sense.
The variable 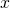$x$ occurs twice: once in the open sentence 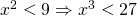$x^2<9 \Rightarrow x^3<27$ , and once in the quantifier.
We could read this aloud as ``If a number's square is less than 9, its cube is less than 27."

One very important trick to do with a bound variable is to replace it, across the board, with another variable. I call this letting go of your $x$ s. So for example, in an integral we can change the integrating variable at whim:

$\int_1^3 x^2\ dx=\frac{26}{3}=\int_1^3 y^2\ dy$

We can do the same with quantified statements and open sentences:

$\forall x, x^2<9 \Rightarrow x^3<27\text{ means the same thing as } \forall q, q^2<9 \Rightarrow q^3<27$

What does all this have to do with sets and set-builder notation? Observe that the variables that appear in set-builder notation are almost all bound, which we can tell because they occur twice (once on each side of the pipe). For example:

$\left\{x\middle\vert -1<x<1\right\}$

is the same set as

$\left\{g\middle\vert -1<g<1\right\}$

which in turn is the same set as

$\left\{t\middle\vert -1<t<1\right\}$

The point is that the particular choice of variable $x$ or $y$ or $Z$ or $p$ or $\varphi$ has no significance at all. By way of example, if $A=\left\{ x \middle\vert x^2 \in[1,3)\right\}$ , then

$t\in A\text{ means that } t^2\in[1,3)$

$F\in A\text{ means that } F^2\in[1,3)$

In particular, our definition of $A$ does not create any particular link between the letter $x$ and the set $A$ . We could just as well have defined $A=\left\{ z \middle\vert z^2 \in[1,3)\right\}$ .

Where are the quantifiers?

Learning to let go of your s

Learning to let go of your $x$ s